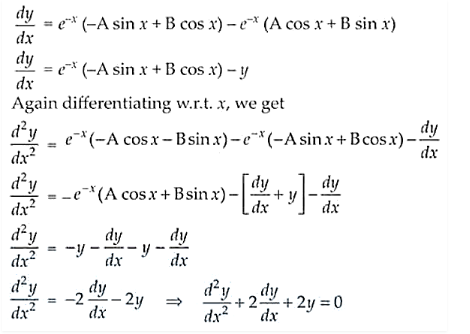Question:
If y = e–x (A cos x + B sin x), then y is a solution of
(A) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
(B) $\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0$
(C) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0$
(D) $\frac{d^{2} y}{d x^{2}}+2 y=0$
Solution:
Correct option is (C).
Given equation, y = e–x (A cos x + B sin x)
Differentiating on both the sides, w.r.t. x, we get