Question:
If $z$ be a complex number satisfying $|\operatorname{Re}(z)|+|\operatorname{Im}(z)|=4$, then $|z|$ cannot be:
Correct Option: , 3
Solution:
$z=x+i y$
$|x|+|y|=4$
$|z|=\sqrt{x^{2}+y^{2}}$ 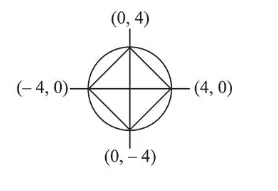
Minimum value of
$|z|=4$
$|z| \in[\sqrt{8}, \sqrt{16}]$
So, $|z|$ can't be $\sqrt{7}$
