In a ∆ABC, it is given that ∠A : ∠B : ∠C = 3 : 2 : 1 and ∠ACD = 90°. If BC is produced to E then ∠ECD = ?
Question:
In a ∆ABC, it is given that ∠A : ∠B : ∠C = 3 : 2 : 1 and ∠ACD = 90°. If BC is produced to E then ∠ECD = ?
(a) 60°
(b) 50°
(c) 40°
(d) 25°
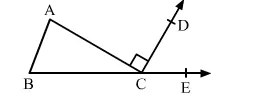
Solution:
Let $\angle A=(3 x)^{\circ}, \angle B=(2 x)^{\circ}$ and $\angle C=x^{\circ}$
Then,
$3 x+2 x+x=180^{\circ} \quad[$ Sum of the angles of a triangle $]$
$\Rightarrow 6 x=180^{\circ}$
$\Rightarrow x=30^{\circ}$
Hence, the angles are
$\angle A=3 \times 30^{\circ}=90^{\circ}, \angle B=2 \times 30^{\circ}=60^{\circ}$ and $\angle C=30^{\circ}$
Side BC of triangle ABC is produced to E.
$\therefore \angle A C E=\angle A+\angle B$
$\Rightarrow \angle A C D+\angle E C D=90^{\circ}+60^{\circ}$
$\Rightarrow 90^{\circ}+\angle E C D=150^{\circ}$
$\Rightarrow \angle E C D=60^{\circ}$
Hence, the correct answer is option (a).
