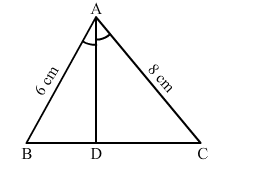
Question:
In a ∆ABC, it is given that AB = 6 cm, AC = 8 cm and AD is the bisector of ∠A. Then, BD : DC =?
(a) 3 : 4
(b) 9 : 16
(c) 4 : 3
(d) $\sqrt{3}: 2$
Solution:
(a) 3 : 4
In $\triangle A B D$ and $\triangle A C D$, we have:
$\angle B A D=\angle C A D$
Now,
$\frac{B D}{D C}=\frac{A B}{A C}=\frac{6}{8}=\frac{3}{4}$
$B D: D C=3: 4$
