Question:
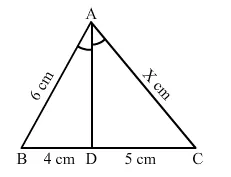
In a ∆ABC, it is given that AD is the internal bisector of ∠A. If BD = 4 cm, DC = 5 cm and AB = 6 cm, then AC = ?
(a) 4.5 cm
(b) 8 cm
(c) 9 cm
(d) 7.5 cm
Solution:
(d) 7.5 cm
It is given that AD bisects angle A.
Therefore, applying angle bisector theorem, we get:
$\frac{B D}{D C}=\frac{A B}{A C}$
$\Rightarrow \frac{4}{5}=\frac{6}{x}$
$\Rightarrow x=\frac{5 \times 6}{4}=7.5$
Hence, AC = 7.5 cm
