In a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively.

We have:
(i)
Let AB and CD be two chords of a circle such that AB is parallel to CD on the same side of the circle.
Given: AB = 8 cm, CD = 6 cm and OB = OD = 5 cm
Join OL and OM.

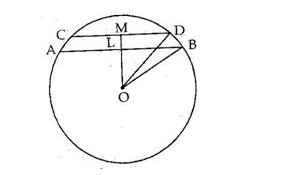
The perpendicular from the centre of a circle to a chord bisects the chord.

$\therefore L B=\frac{A B}{2}=\left(\frac{8}{2}\right)=4 \mathrm{~cm}$

Now, in right angled ΔBLO, we have:
OB2 = LB2 + LO2
⇒ LO2 = OB2 − LB2
⇒ LO2 = 52 − 42  
⇒ LO2 = 25 − 16 = 9
∴ LO = 3 cm

Similarly, $M D=\frac{C D}{2}=\left(\frac{6}{2}\right)=3 \mathrm{~cm}$

In right angled ΔDMO, we have:
OD2 = MD2 + MO2
⇒ MO2 = OD2 − MD2
⇒ MO2   = 52 − 32
⇒ MO2 = 25 − 9 = 16
⇒MO = 4 cm
∴ Distance between the chords = (MO − LO) = (4 − 3) cm = 1 cm

(ii)
Let AB and CD be two chords of a circle such that AB is parallel to CD and they are on the opposite sides of the centre.
Given: AB = 8 cm and CD = 6 cm
Draw OL ⊥ AB and OM ⊥ CD.

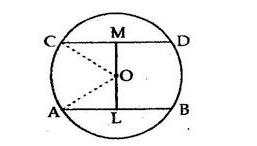
Join OA and OC.
OA = OC = 5 cm (Radii of a circle)
The perpendicular from the centre of a circle to a chord bisects the chord.

$\therefore A L=\frac{A B}{2}=\left(\frac{8}{2}\right)=4 \mathrm{~cm}$

Now, in right angled ΔOLA, we have:
OA2 = AL2 + LO2
⇒ LO2 = OA2 − AL2
⇒ LO2 = 52 − 42  
 ⇒ LO2 = 25 − 16 = 9
∴ LO = 3 cm

Similarly, $C M=\frac{C D}{2}=\left(\frac{6}{2}\right)=3 \mathrm{~cm}$

In right angled ΔCMO, we have:
OC2 = CM2 + MO2
⇒ MO2 = OC2 − CM2
⇒ MO2 = 52 − 32
⇒ MO2 = 25 − 9 = 16
∴ MO = 4 cm
Hence, distance between the chords = (MO + LO) = (4 + 3) cm = 7 cm