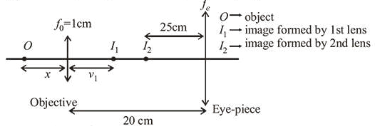
In a compound microscope,

Solution:

$(4.48)$

According to question, final image i.e., $v_{2}=25 \mathrm{~cm}$,

$f_{0}=1 \mathrm{~cm}$, magnification, $m=m_{1} m_{2}=100^{2}$

Using lens formula,

For first lens or objective $=\frac{1}{v_{1}}-\frac{1}{-x}=\frac{1}{1} \Rightarrow v_{1}=\frac{x}{x-1}$

Also magnification $\left|m_{1}\right|=\left|\frac{v_{1}}{u_{1}}\right|=\frac{1}{x-1}$

For 2nd lens or eye-piece, this is acting as object

$\therefore u_{2}=-\left(20-v_{1}\right)=-\left(20-\frac{x}{x-1}\right)$ and $v_{2}=-25 \mathrm{~cm}$

Angular magnification $\left|m_{A}\right|=\left|\frac{D}{u_{2}}\right|=\frac{25}{\left|u_{2}\right|}$

Total magnification $m=m_{1} m_{A}=100$

$\left(\frac{1}{x-1}\right)\left(\frac{25}{20-\frac{x}{x-1}}\right)=100$

$\Rightarrow \frac{25}{20(x-1)-x}=100 \Rightarrow 1=80(x-1)-4 x$

$\Rightarrow 76 x=81 \Rightarrow x=\frac{81}{76}$

$\Rightarrow u_{2}=-\left(20-\frac{\frac{81}{76}}{\frac{81}{76}-1}\right)=\frac{-19}{5}$

Again using lens formula for eye-piece

$\frac{1}{-25}-\frac{1}{-\frac{19}{5}}=\frac{1}{f_{e}} \Rightarrow f_{e}=\frac{25 \times 19}{106} \approx 4.48 \mathrm{~cm}$