In a meter bridge experiment $\mathrm{S}$ is a standard resistance. $R$ is a resistance wire. It is found that balancing length is $l=25 \mathrm{~cm}$. If $\mathrm{R}$ is replaced by a wire of half length and half diameter that of $\mathrm{R}$ of same material, then the balancing distance $l^{\prime}$ (in $\mathrm{cm}$ ) will now be
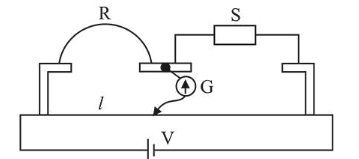
(40) For the given meter bridge
$\frac{R}{S}=\frac{\ell_{1}}{100-\ell_{1}}$ Where, $\ell_{1}=$ balancing length
$\Rightarrow \quad \frac{R}{S}=\frac{25}{75}=\frac{1}{3}$ ....(1)
New resistance,
$R^{\prime}=\frac{\rho \frac{\ell}{2}}{\frac{A}{4}}=\rho \frac{\ell \times 2}{A}$ $\left(\because \mathrm{R}=\rho \frac{\ell}{\mathrm{A}}\right)$
$\Rightarrow R^{\prime}=2 R$
$\frac{R^{\prime}}{S}=\frac{\ell_{2}}{100-\ell_{2}}$
$\Rightarrow \quad \frac{2 R}{S}=\frac{\ell_{2}}{100-\ell_{2}}$
$\Rightarrow \quad 2 \times \frac{1}{3}=\frac{\ell_{2}}{100-\ell_{2}}$ Using (i)
$\Rightarrow \quad \ell_{2}=40 \mathrm{~cm}$
