Question:
In a quadrilateral ABCD, if AO and BO are the bisectors of ∠A and ∠B respectively, ∠C = 70° and ∠D = 30°. Then, ∠AOB = ?
(a) 40°
(b) 50°
(c) 80°
(d) 100°
Solution:
(b) 50o
Explanation:
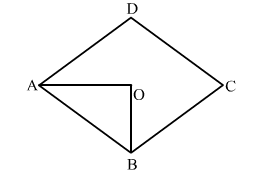
∠C = 70o and ∠D = 30o
Then ∠A + ∠B = 360o - (70 +30)o = 260o
$\therefore \frac{1}{2}(\angle A+\angle B)=\frac{1}{2}\left(260^{\circ}\right)=130^{\circ}$
In ∆ AOB, we have:
$\angle A O B=180^{\circ}-\left[\frac{1}{2}(\angle A+\angle B)\right]$
⇒ ∠AOB = 180 - 130 = 50o
