Question:
In a scries LR circuit, power of $400 \mathrm{~W}$ is dissipated from a source of $250 \mathrm{~V}, 50 \mathrm{~Hz}$. The power factor of the circuit is $0.8$. In order to bring the power factor to unity, a capacitor of value $\mathrm{C}$ is added in series to the $\mathrm{L}$ and $\mathrm{R}$. Taking the value of $\mathrm{C}$ as $\left(\frac{\mathrm{n}}{3 \pi}\right) \mu \mathrm{F}$, then value of $\mathrm{n}$ is
Solution:
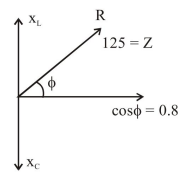
$P=\frac{E_{\text {rms }}^{2}}{Z} \cos \phi$
$400=\frac{(250)^{2} \times 0.8}{Z}$
$Z=25 \times 5=125$
$X_{L}=125 \sin \phi=125 \times 0.6=75$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
