Question:
In a triangle $\mathrm{PQR}$, the co-ordinates of the points $\mathrm{P}$ and $\mathrm{Q}$ are $(-2,4)$ and $(4,-2)$ respectively. If the equation of the perpendicular bisector of $\mathrm{PR}$ is $2 x-y+2=0$, then the centre of the circumcircle of the $\triangle \mathrm{PQR}$ is :
Correct Option: , 2
Solution:
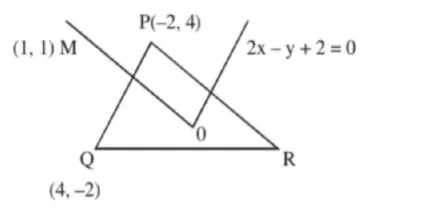
Equation of perpendicular bisector of $P R$ is
$y=x$
Solving with $2 \mathrm{x}-\mathrm{y}+2=0$ will give
$(-2,2)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.