Question:
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
(a) $\mathrm{BC}=\mathrm{CY}$
(b) $B C=B Y$
(c) $B C \neq C Y$
(d) $B C \neq B Y$
Solution:
Given: XY||BC and BY is bisector of ∠XYC.
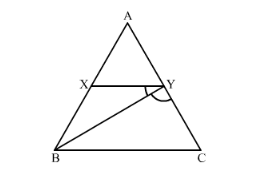
Since XY||BC
So ∠YBC = ∠BYC (Alternate angles)
Now, in triangle BYC two angles are equal. Therefore, the two corresponding sides will be equal.
Hence, BC = CY
Hence option (a) is correct.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
