Question:
In ∆ABC, AB = AC and the bisectors of ∠B and ∠C meet at a point O. Prove that BO = CO and the ray AO is the bisector of ∠A.
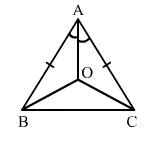
Solution:
In triangle ABC, we have:
AB = AC (Given)
$\Rightarrow \angle B=\angle C$
$\Rightarrow \frac{1}{2} \angle B=\frac{1}{2} \angle C$
$\Rightarrow \angle O B C=\angle O C B$
$\Rightarrow B O=C O$
Now, in $\triangle A O B$ and $\triangle A O C$, we have:
$O B=O C \quad$ (Proved)
$A B=A C \quad$ (Given)
$A O=A O \quad$ (Common)
$\therefore \triangle A O B \cong \triangle A O C \quad$ (SSS criterion)
i.e., $\angle B A O=\angle C A O$ (Corresponding angles of congruent triangles)
So, it shows that ray AO is the bisector of ∠A.
Hence, proved.
