In ∆ABC, AB = AC. Side BC is produced to D. Prove that

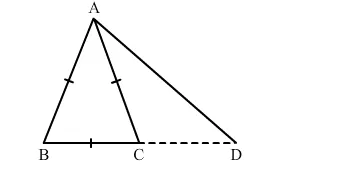
Solution:

Draw $A E \perp B C$ meeting $B C$ at $D$.

Applying Pythagoras theorem in right-angled triangle AED, we get:

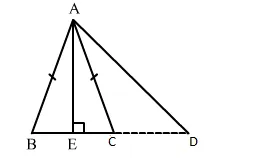
Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.
So, BE = CE
and DE+ CE = DE + BE = BD

$A D^{2}=A E^{2}+D E^{2}$

$\Rightarrow A E^{2}=A D^{2}-D E^{2} \ldots(\mathrm{i})$

In $\triangle A C E$,

$A C^{2}=A E^{2}+E C^{2}$

$\Rightarrow A E^{2}=A C^{2}-E C^{2} \ldots$ (ii)

Using (i) and (ii),

$\Rightarrow A D^{2}-D E^{2}=A C^{2}-E C^{2}$

$\Rightarrow A D^{2}-A C^{2}=D E^{2}-E C^{2}$

$=(D E+C E)(D E-C E)$

$=(D E+B E) C D$

$=B D . C D$