Question:
In ∆ABC and ∆DEF, it is given that AB = DE and BC = EF. In order that ∆ABC ≅ ∆DEF, we must have
(a) ∠A = ∠D
(b) ∠B = ∠E
(c) ∠C = ∠F
(d) none of these
Solution:
(b) $\angle B=\angle E$
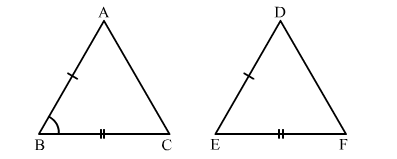
In $\triangle A B C$ and $\triangle D E F$, we have :
AB = DE (Given)
BC = EF (Given)
In order that $\triangle A B C \cong D E F$, we must have $\angle B=\angle E$.
