Question:
In ∆ABC, D and E are the midpoints of AB and AC, respectively. Find the ratio of the areas of ∆ADE and ∆ABC.
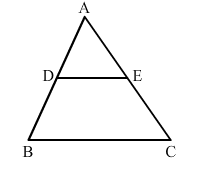
Solution:
It is given that D and E are midpoints of AB and AC.
Applying midpoint theorem, we can conclude that DE
Hence, by B.P.T., we get:
$\frac{A D}{A B}=\frac{A E}{A C}$
Also, $\angle A=\angle A$
Applying SAS similarity theorem, we can conclude that $\triangle A D E \sim \triangle A B C$.
Therefore, the ratio of the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
$\therefore \frac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta A B C)}=\frac{D E^{2}}{B C^{2}}$
$=\frac{\left(\frac{1}{2} B C\right)^{2}}{B C^{2}}$
$=\frac{1}{4}$
