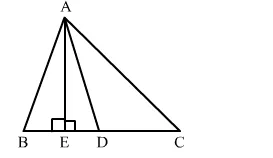
In ∆ABC, D is the midpoint of BC and AE ⊥ BC. If AC > AB, show that

In right-angled triangle AEB, applying Pythagoras theorem, we have:

$A B^{2}=A E^{2}+E B^{2} \quad \ldots$ (i)

In right-angled triangle AED, applying Pythagoras theorem, we have:

$A D^{2}=A E^{2}+E D^{2}$

$\Rightarrow A E^{2}=A D^{2}-E D^{2}$      ....(ii)

Therefore,

$A B^{2}=A D^{2}-E D^{2}+E B^{2} \quad($ from $(\mathrm{i})$ and $(\mathrm{ii}))$

$A B^{2}=A D^{2}-E D^{2}+(B D-D E)^{2}$

$=A D^{2}-E D^{2}+\left(\frac{1}{2} B C-D E\right)^{2}$

$=A D^{2}-D E^{2}+\frac{1}{4} B C^{2}+D E^{2}-B C \cdot D E$

$=A D^{2}+\frac{1}{4} B C^{2}-B C \cdot D E$

This completes the proof.