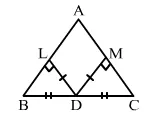
In ∆ABC, D is the midpoint of BC. If DL ⊥ AB and DM ⊥ AC such that DL = DM, prove that AB = AC.

In $\triangle \mathrm{BDL}$ and $\triangle \mathrm{CDM}$, we have:

$\mathrm{BD}=\mathrm{CD} \quad$ (D is midpoint)

$\mathrm{DL}=\mathrm{DM} \quad$ (Given)

$\angle \mathrm{BLD}=\angle \mathrm{CMD} \quad\left(90^{\circ}\right.$ each $)$

Thus, $\triangle \mathrm{BDL} \cong \triangle \mathrm{CDM}$ (RHS criterion)

$\Rightarrow \mathrm{BL}=\mathrm{MC}(\mathrm{CPCT})$

$\therefore \angle B=\angle C$

This makes triangle ABC an isosceles triangle.
Or AB = AC
Hence, proved.