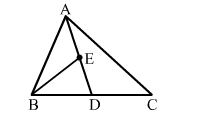
In ∆ABC, if D is the midpoint of BC and E is the midpoint of AD, then ar(∆BED) = ?

(c) $\frac{1}{4} \operatorname{ar}(\triangle A B C)$

Since D is the mid point of BC, AD is a median of ∆ABC and BE is the median of ∆ABD.
We know that a median of a triangle divides it into two triangles of equal areas.

i.e., $\operatorname{ar}(\Delta A B D)=\frac{1}{2} \operatorname{ar}(\Delta A B C)$             (i)

$\Rightarrow \operatorname{ar}(\triangle B E D)=\frac{1}{2} \operatorname{ar}(\triangle A B D)$          ...(ii)

From (i) and (ii), we have:

$\operatorname{ar}(\Delta B E D)=\frac{1}{2} \times \frac{1}{2} \times \operatorname{ar}(\Delta A B C)$

$\therefore \operatorname{ar}(\Delta B E D)=\frac{1}{4} \times \operatorname{ar}(\triangle A B C)$