In △ABC, M and N are points on AB and AC

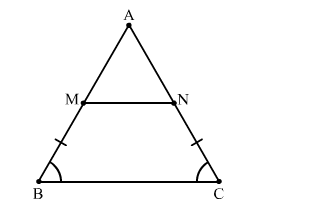
In △ABC, ∠B = ∠C
∴AB = AC (Sides opposite to equal angle are equal)
Subtracting BM from both sides, we get
AB − BM = AC − BM
⇒AB − BM = AC − CN           (∵BM = CN)
⇒AM = AN
∴∠AMN = ∠ANM (Angles opposite to equal sides are equal)
Now, In △ABC,
∠A + ∠B + ∠C = 180o                     .....(1)
                                                               (Angle Sum Property of triangle)
Again In In △AMN,
∠A +∠AMN + ∠ANM = 180o          ......(2)
                                                               (Angle Sum Property of triangle)
From (1) and (2), we get
∠B + ∠C = ∠AMN + ∠ANM
⇒2∠B  = 2∠AMN  
⇒∠B  = ∠AMN
Since, ∠B  and ∠AMN are corresponding angles.
∴ MN∥BC