In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.

In $\triangle A B C, P$ and $Q$ are points on sides $A B$ and $A C$ respectively such that $P Q \| B C$

Then we have

$\frac{A P}{A B}=\frac{A Q}{A C}$

$A P=3 \mathrm{~cm}, P B=5 \mathrm{~cm}, A C=8 \mathrm{~cm}$ and $A B=8 \mathrm{~cm}$

$\frac{3}{8}=\frac{A Q}{8}$

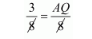
$3=A Q$

Hence the value of $A Q$ is $3 \mathrm{~cm}$