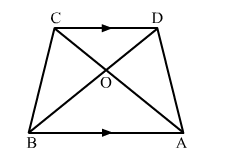
In an trapezium ABCD, it is given that AB ∥ CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(∆AOB) = 84 cm2. Find ar(∆COD).
In ∆AOB and ∆COD, we have:
$\angle A O B=\angle C O D($ Vertically opposite angles $)$
$\angle \mathrm{OAB}=\angle \mathrm{OCD}$ (Alternate angles as $\mathrm{AB} \| \mathrm{CD}$ )
Applying AA similiarity criterion, we get:
$\triangle \mathrm{AOB} \sim \triangle \mathrm{COD}$
$\therefore \frac{a r(\triangle A O B)}{a r(\triangle C O D)}=\frac{A B^{2}}{C D^{2}}$
$\Rightarrow \frac{84}{a r(\triangle C O D)}=\left(\frac{A B}{C D}\right)^{2}$
$\Rightarrow \frac{84}{a r(\triangle C O D)}=\left(\frac{2 C D}{C D}\right)^{2}$
$\Rightarrow \operatorname{ar}(\triangle C O D)=\frac{84}{4}=21 \mathrm{~cm}^{2}$
