In Fig. 1, PQ and PR are tangents to the circle

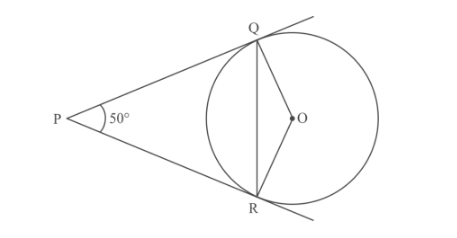
We are given the below figure in which

PQ and PR are tangents to the circle with centre O and 

We have to find 

PQ is the tangent to circle

Therefore  [Since Radius of a circle is perpendicular to tangent]

Similarly

We know that sum of angles of a quadrilateral

Therefore in Quadrilateral PQOR

$\angle Q P R+\angle P R O+\angle R O Q+\angle O Q P=360^{\circ}$

$50^{\circ}+90^{\circ}+\angle R O Q+90^{\circ}=360^{\circ}$

$\angle R O Q=360^{\circ}-230^{\circ}$

$\angle R O Q=130^{\circ}$

In $\Delta O Q R$

$O Q=O R$  [Radius of same circle]

Therefore $\triangle O Q R$ is isosceles triangle

Hence $\angle \mathrm{ORQ}=\angle \mathrm{OQR}$ [Angles opposite to equal sides of isosceles triangle]

In $\triangle O Q R$

$\angle R O Q+\angle O Q R+\angle Q R O=180^{\circ}\left[\right.$ Sum of angles of a triangle $\left.=180^{\circ}\right]$

$2 \angle O Q R+130^{\circ}=180^{\circ}$

$\angle O Q R=\frac{50^{\circ}}{2}$

$=25^{\circ}$

Hence option (a) is correct.