In fig. (10).23, PQRS is a square and SRT is an equilateral triangle. Prove that (i) PT = QT (ii) ∠TQR = 15°

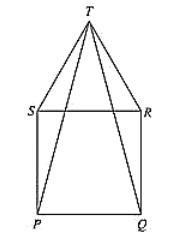
Given that PQRS is a square and SRT is an equilateral triangle. And given to prove that

(i) PT = QT and (ii) ∠TQR = 15°

Now, PQRS is a square

PQ = QR = RS = SP ... (i)

And ∠SPQ = ∠PQR = ∠QRS = ∠RSP = 90° = right angle

And also, SRT is an equilateral triangle.

SR = RT = TS ... (ii)

And ∠TSR = ∠SRT = ∠RTS = 60°

From (i) and (ii)

PQ = QR = SP = SR = RT = TS  .... (iii)

And also,

∠TSP =  ∠TSR + ∠RSP = 60° + 90° + 150°

∠TRQ = ∠TRS + ∠SRQ = 60° + 90° + 150°

⟹ ∠TSR = ∠TRQ = 150°   ...  (iv)

SP = RQ           [From (iii)]

So, by SAS congruence criterion we have

ΔTSP = ΔTRQ

PT = QT   [Corresponding parts of congruent triangles are equal] Consider ΔTQR.

QR = TR        [From (iii)]

ΔTQR is a isosceles triangle.

∠QTR = ∠TQR [angles opposite to equal sides]

Now,

Sum of angles in a triangle is equal to 180∘

⟹ ∠QTR + ∠TQR + ∠TRQ = 180°

⟹ 2∠ TQR + 150° = 180°     [From (iv)]

⟹ 2∠TQR = 180° - 150°

⟹ 2∠ TQR = 30°                         ∠TQR = 15°] ...

Hence proved