In Fig. 5, DE || AC and DF || AE.

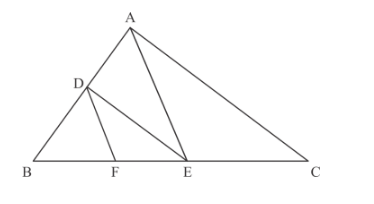
Given that:

If DE||AC and DF||AE, then we have to prove that

$\frac{E F}{B F}=\frac{E C}{B E}$

The following given figure is

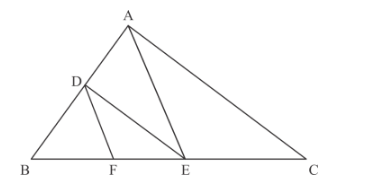
We can easily see that in the given figure the triangle BDF and triangle BAE are similar triangles and also the triangle BDE and triangle BAC are similar triangles. Now we are applying the theorem of similar triangle in triangle BDF and triangle BAE, we get

$\frac{B F}{E F}=\frac{B D}{D A}$......(1)

Similarly in triangle BDE and triangle BAC, we get

$\frac{B E}{E C}=\frac{B D}{D A}$......(2)

Now we are comparing the equation (1) and (2), we have

$\frac{B F}{E F}=\frac{B E}{E C}$

Now take the reciprocal of the above equation, we have

$\frac{E F}{B F}=\frac{E C}{B E}$

Hence we have proved that   $\frac{E F}{B F}=\frac{E C}{B E}$