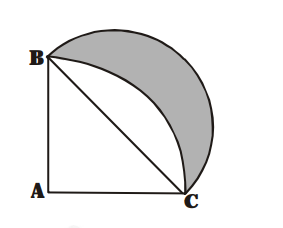
In fig., ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter.

$\mathrm{BC}=\sqrt{(14)^{2}+(14)^{2}}=14 \sqrt{2} \mathrm{~cm}$

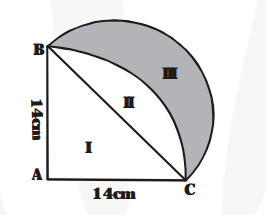
Area of region II = Area of sector $\mathrm{ABC}$

- Area of $\triangle \mathrm{ABC}=\left\{\frac{1}{4} \pi \times(14)^{2}-\frac{1}{2} \times 14 \times 14\right\} \mathrm{cm}^{2}$

$=\left\{\frac{1}{4} \times \frac{22}{7} \times 196-93\right\} \mathrm{cm}^{2}=56 \mathrm{~cm}^{2}$

The area of the shaded region III = The area of the semicircle drawn on $\mathrm{BC}$ as diameter The area of region II

$=\left\{\frac{1}{2} \pi \times\left(\frac{14 \sqrt{2}}{2}\right)^{2}-56\right\} \mathrm{cm}^{2}$

$=\left\{\frac{1}{2} \times \frac{22}{7} \times 98-56\right\} \mathrm{cm}^{2}$

$=\{154-56\} \mathrm{cm}^{2}=98 \mathrm{~cm}^{2}$