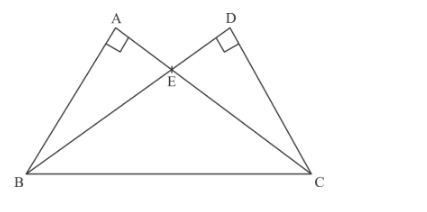
In Figure 4, two triangles ABC and DBC are on the

Given that, there are two triangles ABC and DBC are on the same base BC in which
∠A = ∠D = 90°. If CA and BD meet each other at E, then we have to prove that AE × CE = BE × DE

The following figure is given

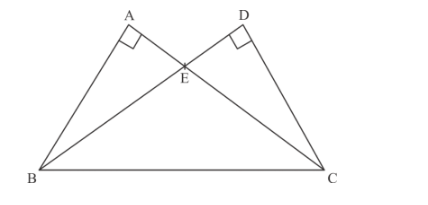
From the above figure, we can easily see that $\triangle A B E$ and $\triangle D C E$ are similar triangles, therefore we can use the property of similar triangle.

$\frac{A E}{D E}=\frac{B E}{C E}$

Hence $A E \times C E=B E \times E D$