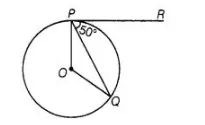
In figure, if 0 is the centre of a circle,

(a) Given, ∠QPR = 50°

We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.

$\therefore \quad \angle O P R=90^{\circ}$

$\Rightarrow \quad \angle O P Q+\angle Q P R=90^{\circ} \quad$ [from figure]

$\Rightarrow \quad \angle O P Q=90^{\circ}-50^{\circ}=40^{\circ} \quad\left[\because \angle Q P R=50^{\circ}\right]$

Now, $O P=O Q=$ Radius of circle

$\therefore \quad \angle O Q P=\angle O P Q=40^{\circ}$

[since, angles opposite to equal sides are equal]

$\ln \triangle O P Q_{1} \quad \angle O+\angle P+\angle Q=180^{\circ}$

[since, sum of angles of a triangle $=180^{\circ}$ ]

$\Rightarrow \quad \angle O=180^{\circ}-\left(40^{\circ}+40^{\circ}\right) \quad\left[\because \angle P=40^{\circ}=\angle Q\right]$

$=180^{\circ}-80^{\circ}=100^{\circ}$