In given figure,

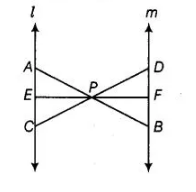
Given $l \| m$ and line segments $A B, C D$ and $E F$ are concurrent at point $P$.

To prove $\frac{A E}{B F}=\frac{A C}{B D}=\frac{C E}{F D}$

Proof in $\triangle \mathrm{APC}$ and $\triangle B P D$.$\angle A P C=\angle B P D$ [vertically opposite angles]

$\angle P A C=\angle P B D$ [alternate angles]

$\therefore$ $\triangle A P C \sim \triangle B P D$ [by AAA similarity criterion]

Then, $\frac{A P}{P B}=\frac{A C}{B D}=\frac{P C}{P D}$ $\ldots($ i)

In $\triangle A P E$ and $\triangle B P F$, $\angle A P E=\angle B P F$ [vertically opposite angles]

$\angle P A E=\angle P B F$ [alternate angles]

$\therefore$ $\triangle A P E \sim \triangle B P F$ [by AAA similarity criterion]

Then, $\frac{A P}{P B}=\frac{A E}{B F}=\frac{P E}{P F}$  ...(ii)

 In $\triangle P E C$ and $\triangle P F D$, $\angle E P C=\angle F P D$ [vertically opposite angles]  

$\angle P C E=\angle P D F$ [alternate angles]

$\triangle P E C \sim \triangle P F D \quad$ [by AAA similarity criterion]

Then, $\frac{P E}{P F}=\frac{P C}{P D}=\frac{E C}{F D}$ .....(iii)

From Eqs. (i), (ii) and (iii),

$\frac{A P}{P B}=\frac{A C}{B D}=\frac{A E}{B F}=\frac{P E}{P F}=\frac{E C}{F D}$

$\therefore$ $\frac{A E}{B F}=\frac{A C}{B D}=\frac{C E}{F D}$ Hence proved.