In ΔPQR and ΔMST,

False
We know that, the sum of three angles of a triangle is 180°.

In ΔPQR,                                     ∠P + ∠Q + ∠R = 180°

⇒                                              55° + 25° + ∠R = 180°

⇒                                   ∠R = 180° – (55° + 25°)= 180° – 80° =100°

In ΔTSM,                                    ∠T + ∠S + ∠M = 180°

⇒                                               ∠T + ∠25°+ 100° = 180°

⇒                                                                    ∠T = 180°-(25° +100°)

=180°-125°= 55°

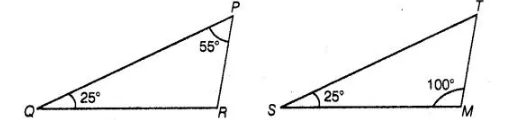
In ΔPQR and A TSM, and

∠P = ∠T, ∠Q = ∠S,

and                                                        ∠R = ∠M

ΔPQR ~ ΔTSM [since, all corresponding angles are equal]

Hence, Δ QPR is not similar to ΔTSM, since correct correspondence is P ↔ T, Q < r→ S and R ↔M