In Q.No. 1, if PB = 10 cm, what is the perimeter of Δ PCD?

Here, we have to find the perimeter of triangle PCD.

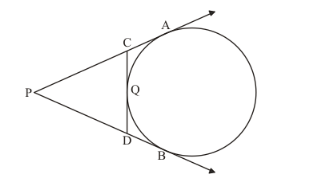
Perimeter is nothing but sum of all sides of the triangle. Therefore we have,

Perimeter of  = 

In the given figure we can see that,

 = 

Therefore,

Perimeter of  = 

We know that the two tangents drawn to a circle from a common external point will be equal in length. From this property we have,

$\mathrm{CQ}=\mathrm{CA}$

$\mathrm{QD}=\mathrm{DB}$

Now let us replace CQ and QD with CA and DA. We get,

Perimeter of  = 

Also from the figure we can see that,

$\mathrm{DB}+\mathrm{PD}=\mathrm{PB}$

$\mathrm{PC}+\mathrm{CA}=\mathrm{PA}$

Now, let us replace these in the equation for perimeter of. We have,

Perimeter of  = PB +PA

Also, from the property of tangents we know that, two tangents drawn to a circle from the same external point will be equal in length. Therefore,

PB = PA

Let us replace PA with PB in the above equation. We get,

Perimeter of  = 2PB

It is given in the question that PB = 10 cm. Therefore,

Perimeter of  = 

Perimeter of  = 20 cm

Hence, the perimeter of is 20 cm.