Question:
In the adjoining figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisector of ∠BAC.
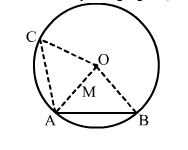
Solution:
Given: AB and AC are two equal chords of a circle with centre O.
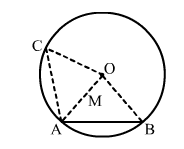
To prove: ∠OAB = ∠OAC
Construction: Join OA, OB and OC.
Proof:
In ΔOAB and ΔOAC, we have:
AB = AC (Given)
OA = OA (Common)
OB = OC (Radii of a circle)
∴ Δ OAB ≅ Δ OAC (By SSS congruency rule)
⇒ ∠OAB = ∠OAC (CPCT)
Hence, point O lies on the bisector of ∠BAC.
