In the adjoining figure, $A B C D$ is a parallelogram. If $P$ and $Q$ are points on $A D$ and $B C$ respectively such that $A P=\frac{1}{3} A D$ and $C Q=\frac{1}{3} B C$, prove that $A Q C P$ is a parallelogram.
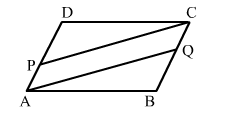
We have:
∠B = ∠D [Opposite angles of parallelogram ABCD]
AD = BC and AB = DC [Opposite sides of parallelogram ABCD]
Also, AD || BC and AB|| DC
It is given that $A P=\frac{1}{3} A D$ and $C Q=\frac{1}{3} B C$.
∴ AP = CQ [∵ AD = BC]
In ∆DPC and ∆BQA, we have:
AB = CD, ∠B = ∠D and DP = QB $\left[\because D P=\frac{2}{3} A D\right.$ and $\left.Q B=\frac{2}{3} B C\right]$
i.e., ∆DPC ≅ ∆BQA
∴ PC = QA
Thus, in quadrilatreal AQCP, we have:
AP = CQ ...(i)
PC = QA ...(ii)
∴ AQCP is a parallelogram.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.