Question:
In the adjoining figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
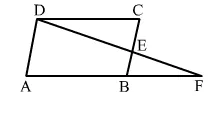
Solution:
Given: ABCD is a parallelogram.
BE = CE (E is the mid point of BC)
DE and AB when produced meet at F.
To prove: AF = 2AB
Proof:
In parallelogram ABCD, we have:
AB || DC
∠DCE = ∠EBF (Alternate interior angles)
In ∆DCE and ∆BFE, we have:
∠DCE = ∠EBF (Proved above)
∠DEC = ∠BEF (Vertically opposite angles)
Also, BE = CE (Given)
∴ ∆DCE ≅ ∆BFE (By ASA congruence rule)
∴ DC = BF (CPCT)
But DC = AB, as ABCD is a parallelogram.
∴ DC = AB = BF ...(i)
Now, AF = AB + BF ...(ii)
From (i), we get:
AF = AB + AB = 2AB
Hence, proved.
Also, BE = CE (Given)
∴ ∆DCE ≅ ∆BFE (By ASA congruence rule)
∴ DC = BF (CPCT)
But DC = AB, as ABCD is a parallelogram.
∴ DC = AB = BF ...(i)
Now, AF = AB + BF ...(ii)
From (i), we get:
AF = AB + AB = 2AB
Hence, proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.