Question:
In the adjoining figure, ABCD is a parallelogram in which AB is produced to E so that BE = AB. Prove that ED bisects BC.
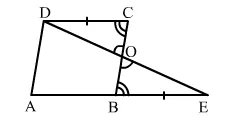
Solution:
In ∆ODC and ∆OEB, we have:
DC = BE (∵ DC = AB)
∠COD = ∠BOE (Vertically opposite angles)
∠OCD = ∠OBE ( Alternate interior angles)
i.e., ∆ODC ≅ ∆OEB
⇒ OC = OB (CPCT)
We know that BC = OC + OB.
∴ ED bisects BC.
