Question:
In the adjoining figure, ABCD is a parallelogram in which ∠DAB = 80° and ∠DBC = 60°. Calculate ∠CDB and ∠ADB.
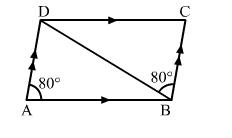
Solution:
Given: ABCD is parallelogram and ∠DAB = 80° and ∠DBC = 60°
To find: Measure of ∠CDB and ∠ADB
In parallelogram ABCD, AD || BC
∴ ∠DBC = ∠ ADB = 60o (Alternate interior angles) ...(i)
As ∠DAB and ∠ADC are adajcent angles, ∠DAB + ∠ADC = 180o
∴ ∠ADC = 180o − ∠DAB
⇒∠ADC = 180o − 80o = 100o
Also, ∠ADC = ∠ADB + ∠CDB
∴ ∠ADC = 100o
⇒ ∠ADB + ∠CDB = 100o ...(ii)
From (i) and (ii), we get:
60o + ∠CDB = 100o
⇒ ∠CDB = 100o − 60o = 40o
Hence, ∠CDB = 40o and ∠ADB = 60o
