Question:
In the adjoining figure, ABCD is a parallelogram whose diagonals intersect each other at O. A line segment EOF is drawn to meet AB at E and DC at F. Prove that OE = OF.
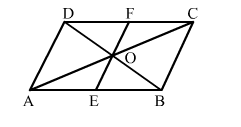
Solution:
In ∆ODF and ∆OBE, we have:
OD = OB (Diagonals bisects each other)
∠DOF = ∠BOE (Vertically opposite angles)
∠FDO = ∠OBE (Alternate interior angles)
i.e., ∆ODF ≅ ∆OBE
∴ OF = OE (CPCT)
Hence, proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.