Question:
In the adjoining figure, ABCD is a quadrilateral in which diag. BD = 14 cm. If AL ⊥ BD and CM ⊥ BD such that AL = 8 cm and CM = 6 cm, find the area of quad. ABCD.
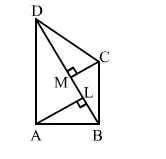
Solution:
$\operatorname{ar}($ quad $A B C D)=\operatorname{ar}(\triangle A B D)+\operatorname{ar}(\triangle B D C)$
$=\frac{1}{2} \times B D \times A L+\frac{1}{2} \times B D \times C M$
$=\frac{1}{2} \times B D \times(A L+C M)$
By substituting the values, we have;
$\operatorname{ar}($ quad $A B C D)=\frac{1}{2} \times 14 \times(8+6)$
= 7 ⨯14
$=98 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.