Question:
In the adjoining figure, CE || AD and CF || BA. Prove that ar(∆CBG) = ar(∆AFG).
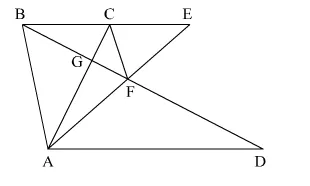
Solution:
$\operatorname{ar}(\triangle \mathrm{CFA})=\operatorname{ar}(\triangle \mathrm{CFB})$ (Triangles on the same base CF and between the same parallels CF || BA will be equal in area)
$\Rightarrow \operatorname{ar}(\triangle$ CFA $)-\operatorname{ar}(\triangle$ CFG $)=\operatorname{ar}(\triangle$ CFB $)-\operatorname{ar}(\triangle$ CFG $)$
$\Rightarrow \operatorname{ar}(\triangle \mathrm{AFG})=\operatorname{ar}(\triangle \mathrm{CBG})$
Hence Proved
