In the adjoining figure, chords AC and BD of a circle with centre O,

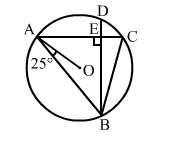
OA = OB (Radii of a circle)
Thus, ∠OBA = ∠OAB = 25°
Join OB.

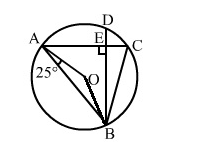
Now in ΔOAB, we have:
∠OAB + ∠OBA + ∠AOB = 180° (Angle sum property of a triangle)
⇒">⇒⇒25° + 25° + ∠AOB = 180°
⇒">⇒⇒50° + ∠AOB = 180°
⇒">⇒⇒∠AOB = (180° – 50°) = 130°

We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by the arc at any point on the circumference.
i.e., ∠AOB = 2∠ACB

$\Rightarrow \angle A C B=\frac{1}{2} \angle A O B=\left(\frac{1}{2} \times 130^{\circ}\right)=65^{\circ}$

Here,∠ACB = ∠ECB
∴ ∠ECB = 65°   ...(i)

Considering the right angled ΔBEC, we have:
∠EBC + ∠BEC + ∠ECB = 180°     (Angle sum property of a triangle)
⇒">⇒⇒∠EBC + 90° + 65° = 180°    [From(i)]
⇒">⇒⇒∠EBC = (180° – 155°) = 25°
Hence, ∠EBC = 25°