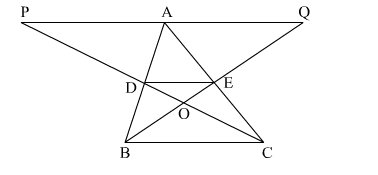
Question:
In the adjoining figure, D and E are respectively the midpoints of sides AB and AC of ∆ABC. If PQ || BC and CDP and BEQ are straight lines then prove that ar(∆ABQ) = ar(∆ACP).
Solution:
In $\triangle \mathrm{PAC}$
PA || DE and E is the midpoint of AC
So, D is the midpoint of PC by converse of midpoint theorem.
Also, $\mathrm{DE}=\frac{1}{2} \mathrm{PA}$ ........(i)
Similarly, $\mathrm{DE}=\frac{1}{2} \mathrm{AQ}$ ...........(ii)
From (1) and (2) we have
PA = AQ
∆ABQ and ∆ACP are on same base PQ and between same parallels PQ and BC
ar(∆ABQ) = ar(∆ACP)
