In the adjoining figure, O is the centre of a circle.

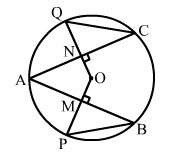
Given: AB and AC are chords of the circle with centre O. AB = AC, OP ⊥ AB and OQ ⊥ AC

To prove: PB = QC
Proof:
AB = AC      (Given)

$\Rightarrow \frac{1}{2} \mathrm{AB}=\frac{1}{2} \mathrm{AC}$

The perpendicular from the centre of a circle to a chord bisects the chord.
∴ MB = NC            ...(i)
Also, OM = ON    (Equal chords of a circle are equidistant from the centre)
 and OP = OQ (Radii)
⇒ OP - OM = OQ - ON
∴ PM = QN          ...(ii)
Now, in ΔMPB and ΔNQC, we have:
MB = NC                [From (i)]
∠PMB = ∠QNC     [90° each]
PM = QN                [From (ii)]
i.e., ΔMPB ≅ ΔNQC    (SAS criterion)
∴ PB = QC        (CPCT)