In the adjoining figure, show that ABCD is a parallelogram.

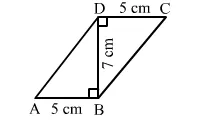
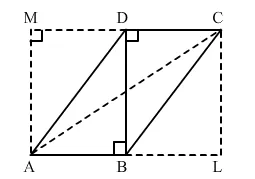
Given: A quadrilateral ABCD and BD is a diagonal.
To prove: ABCD is a parallelogram.
Construction: Draw AM ⊥ DC and CL ⊥ AB   (extend DC and AB). Join AC, the other diagonal of ABCD.

Proof: ar(quad. ABCD) = ar(∆ABD) + ar(​∆DCB)
 = 2 ar(​∆ABD)                    [∵ ar​(∆ABD) = ar(​∆DCB)]

$\therefore \operatorname{ar}(\Delta A B D)=\frac{1}{2} \operatorname{ar}($ quad. $A B C D)$     ...(i)

Again, ar(quad. ABCD) = ar(∆ABC) + ar(​∆CDA)
= 2 ar(​∆ ABC)                    [∵ ar​(∆ABC) = ar(​∆CDA)]

$\therefore \operatorname{ar}(\Delta A B C)=\frac{1}{2} \operatorname{ar}($ quad. $A B C D)$   ...(ii)

From (i) and (ii), we have:

$\operatorname{ar}(\Delta A B D)=\operatorname{ar}(\Delta A B C)=\frac{1}{2} \mathrm{AB} \times \mathrm{BD}=\frac{1}{2} \mathrm{AB} \times \mathrm{CL}$

 ⇒ CL = BD
 ⇒ DC |​​| AB
Similarly, AD |​​| BC.
Hence, ABCD is a paralleogram.
∴ ar(​|​| gm ABCD) = base ​⨯ height = 5 ​⨯ 7 = 35 cm2