In the figure given below, P and Q are centres of two circles, intersecting at B and C, and ACD is a straight line.
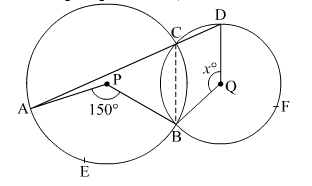
If ∠APB = 150° and ∠BQD = x°, find the value of x.
We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it on the remaining part of the circle.
Here, arc AEB subtends ∠APB at the centre and ∠ACB at C on the circle.
∴ ∠APB = 2∠ACB
$\Rightarrow \angle A C B=\frac{150^{\circ}}{2}=75^{\circ}$ ...(1)
Since ACD is a straight line, ∠ACB + ∠BCD = 180∘
⇒ ∠BCD = 180∘ − 75∘
⇒ ∠BCD = 105∘ ...(2)
Also, arc BFD subtends reflex ∠BQD at the centre and ∠BCD at C on the circle.
∴ reflex ∠BQD = 2∠BCD
$\Rightarrow$ reflex $\angle B Q D=2\left(105^{\circ}\right)=210^{\circ}$ ...(3)
Now,
reflex ∠BQD + ∠BQD = 360∘
⇒ 210∘ + x = 360∘
⇒ x = 360∘ − 210∘
⇒ x = 150∘
Hence, x = 150∘.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
