Question:
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
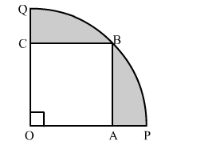
Solution:
Construction: Join OB
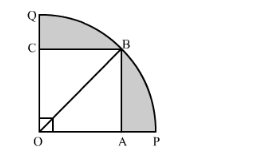
In right triangle AOB
$\mathrm{OB}^{2}=\mathrm{OA}^{2}+\mathrm{AB}^{2}$
$=21^{2}+21^{2}$
$=441+441$
$=882$
$\therefore \mathrm{OB}^{2}=882$
Area of the shaded region = Area of quadrant OPBQ − Area of Square OABC
$=\frac{1}{4} \pi(\mathrm{OB})^{2}-(\mathrm{OA})^{2}$
$=\frac{1}{4} \times \frac{22}{7} \times 882-441$
$=693-441$
$=252 \mathrm{~cm}^{2}$
Hence, the area of the shaded region is 252 cm2.
