In the following figure, AB and CD are two diameters of a

Solution:

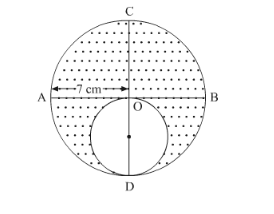
It is given that AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of small circle.

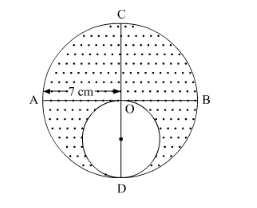
It is given that, $\mathrm{OA}=7 \mathrm{~cm}$'

So, radius r of small circle is

$r=\frac{7}{2} \mathrm{~cm}$

$=3.5 \mathrm{~cm}$

We know that the area $A$ of circle of radius $r$ is $A=\pi r^{2}$.

 

Substituting the value of $r$ in above formula,

$A=\frac{22}{7} \times 3.5 \times 3.5$

$=38.5 \mathrm{~cm}^{2}$

Now, let the area of large circle be $A^{\prime}$.

 

Using the value radius $\mathrm{OA}$,

$A^{\prime}=\frac{22}{7} \times 7 \times 7$

$=154 \mathrm{~cm}^{2}$

Hence,

Area of shaded region =Area of large circle - Area of small circle

$=154-38.5$

$=115.5 \mathrm{~cm}^{2}$