In the following figure, ABC is a right angled triangle in which

Solution:

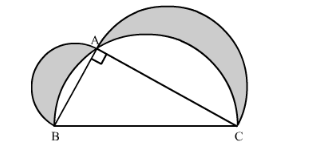
We have given three semi-circles and one right angled triangle.

$\therefore$ Area of shaded region $=$ Area of semi-circle with $\mathrm{AB}$ as a diameter

+ Area of semi-circle with $\mathrm{AC}$ as a diameter

+ Area of right angled $\mathrm{ABC}$

 

- Area of semi-circle with $\mathrm{BC}$ as a diameter

Let us calculate the area of the semi-circle with AB as a diameter.

Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi r^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi\left(\frac{21}{2}\right)^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi}{2}\left(\frac{21}{2}\right)^{2}$

Now we will find the area of the semi-circle with AC as a diameter.

Area of semi-circle with $\mathrm{AC}$ as a diameter $=\frac{\pi r^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi\left(\frac{28}{2}\right)^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi}{2}\left(\frac{28}{2}\right)^{2}$

Now we will find the length of BC.

In right angled triangle ABC, we will use Pythagoras theorem,

$B C^{2}=A B^{2}+A C^{2}$

$\therefore B C^{2}=21^{2}+28^{2}$

$\therefore B C^{2}=441+784$

$\therefore B C^{2}=1225$

 

$\therefore B C=35$

Now we will calculate the area of the right angled triangle ABC.

$A(\triangle A B C)=\frac{1}{2} \times A B \times A C$

$\therefore A(\triangle A B C)=\frac{1}{2} \times 21 \times 28$

$\therefore A(\triangle A B C)=21 \times 14$

 

$\therefore A(\triangle A B C)=294$

Now we will find the area of the semi-circle with BC as a diameter.

Area of semi-circle with $\mathrm{BC}$ as a diameter $=\frac{\pi r^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi\left(\frac{35}{2}\right)^{2}}{2}$

$\therefore$ Area of semi-circle with $\mathrm{AB}$ as a diameter $=\frac{\pi}{2}\left(\frac{35}{2}\right)^{2}$

Now we will substitute all these values in equation (1).

$\therefore$ Area of the shaded region $=\frac{\pi}{2}\left(\frac{21}{2}\right)^{2}+\frac{\pi}{2}\left(\frac{28}{2}\right)^{2}+294-\frac{\pi}{2}\left(\frac{35}{2}\right)^{2}$

$\therefore$ Area of the shaded region $=\frac{\pi}{8}\left(21^{2}+28^{2}-35^{2}\right)+294$

$\therefore$ Area of the shaded region $=\frac{\pi}{8}(441+784-1225)+294$

$\therefore$ Area of the shaded region $=\frac{\pi}{8}(1225-1225)+294$

$\therefore$ Area of the shaded region $=294$

Therefore, area of shaded region is $294 \mathrm{~cm}^{2}$