Question:
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
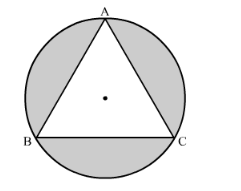
Solution:
We have to find the area of the shaded portion. We have $\triangle \mathrm{ABC}$ which is an equilateral triangle and $\mathrm{AB}=6 \mathrm{~cm}$. Let $r$ be the radius of the circle.
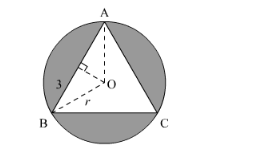
We have O as the circumcentre.
$\angle \mathrm{OBA}=30^{\circ}$
So,
$\cos \left(30^{\circ}\right)=\frac{3}{r}$
Thus, $r=2 \sqrt{3}$
So area of the shaded region,
$=$ Area of the circle $-a r(\triangle \mathrm{ABC})$
$=(3.14)(2 \sqrt{3})^{2}-\frac{\sqrt{3}}{4}(6)^{2}$
$=(37.68-15.59) \mathrm{cm}^{2}$
