In the following figure, O is the centre of a circular arc and AOB is a straight line.

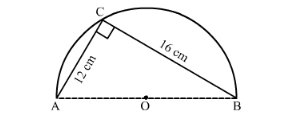
(i) Let us find the perimeter of the shaded region.

$\therefore$ Perimeter $=\pi \times 10+12+16$

$\therefore$ Perimeter $=3.142 \times 10+28$

$\therefore$ Perimeter $=31.42+28$

$\therefore$ Perimeter $=59.42$

Therefore, perimeter of the shaded region is $59.4 \mathrm{~cm}$

Now we will find the area of the shaded region can be calculated as shown below,

Area of the shaded region = Area of the semi-circle − area of the right angled triangle

First, we will find the length of AB as shown below,

$A B^{2}=A C^{2}+C B^{2}$

$\therefore A B^{2}=12^{2}+16^{2}$

$\therefore A B^{2}=144+256$

$\therefore A B^{2}=400$

$\therefore A B=20$

$\therefore$ Area of the shaded region $=\frac{\pi \times 10 \times 10}{2}-\frac{1}{2} \times 12 \times 16$

$\therefore$ Area of the shaded region $=\pi \times 50-6 \times 16$

$\therefore$ Area of the shaded region $=\pi \times 50-96$

Substituting $\pi=3.142$ we get,

$\therefore$ Area of the shaded region $=3.142 \times 50-96$

$\therefore$ Area of the shaded region $=157.1-96$

$\therefore$ Area of the shaded region $=61.1$

Therefore, area of the shaded region is $61.1 \mathrm{~cm}^{2}$.