In the following figure, shows a sector of a circle,

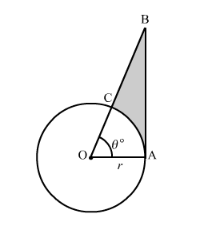
It is given that the radius of circle is $r$ and the angle $\angle A O C=\theta^{\circ}$.

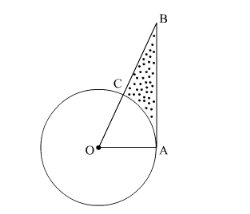
In $\triangle A O B$

It is given that $O A=r$.

$\cos \theta=\frac{O A}{O B}$

$O B=\frac{O A}{\cos \theta}$

$O B=r \sec \theta$

$\tan \theta=\frac{A B}{O A}$

$A B=O A \tan \theta$

$A B=r \tan \theta$

(i) We know that the arc length l of a sector of an angle θ in a circle of radius r is

$l=\frac{\theta}{360^{\circ}} \times 2 \pi r$

Perimeter of sector $A O C=O C+O A+\operatorname{arc}$ length $A B$

Now we substitute the value of OC, OA and l to find the perimeter of sector AOC,

Perimeter of sector $A O C=r+r+\frac{\theta}{360^{\circ}} \times 2 \pi r$

$=2 r+\frac{\theta}{180^{\circ}} \times \pi r$

Perimeter of $\triangle A O B=O B+O A+A B$

$=r \sec \theta+r+r \tan \theta$

$=r(\sec \theta+\tan \theta+1)$

Perimeter of shaded region $A B C=$ Perimeter of $\triangle A O B$ - Perimeter of sector $A O C$

$=r(\sec \theta+\tan \theta+1)-2 r-\frac{\theta}{180^{\circ}} \times \pi r$

$=r\left(\sec \theta+\tan \theta-\frac{\pi \theta}{180^{\circ}}-1\right)$

Hence,  Perimeter of shaded region $A B C=r\left(\sec \theta+\tan \theta-\frac{\pi \theta}{180^{\circ}}-1\right)$

(ii) We know that area $A$ of the sector at an angle $\theta$ in the circle of radius $r$ is

$A=\frac{\theta}{360^{\circ}} \times \pi r^{2}$

Thus

Area of sector $A O C=\frac{\theta}{360^{\circ}} \pi r^{2}$

Area of $\triangle A O B=\frac{1}{2} \times O A \times A B$

$=\frac{1}{2} \times r \times r \tan \theta$

$=\frac{1}{2} \times r^{2} \tan \theta$

Area of shaded region $A B C=$ Area of $\triangle A O B$ - Area of sector $A O C$

$=\frac{1}{2} r^{2} \tan \theta-\frac{\theta}{360^{\circ}} \times \pi r^{2}$

$=\frac{r^{2}}{2}\left(\tan \theta-\frac{\pi \theta}{180^{\circ}}\right)$

Hence, Area of shaded region $A B C=\frac{r^{2}}{2}\left(\tan \theta-\frac{\pi \theta}{180^{\circ}}\right)$